电路中的无源元件：电阻、电容和电感元件

工程上的用电设备和元件是多种多样的，但相当多的部分可 以用电阻元件、电容元件和电感元件的组合（串联、并联或混 联）作出其电路模型，并用电阻、电容和电感三种电路参数来表示。电路参数就是表示电路元件性质的物理量。

事实上，电路参数与实际电气设备是不完全相同的。例如，电子电路常用的电感线圈其主要特性是电感性，但严格地说，电感线圈是金属导线制成的，本身还有电阻；当电流流过电感线圈时，还会形成电场，所以还应考虑电容这个参数。但工程上常突出设备和元件的主要电磁性能，而忽略次要因素。因此，我们所讨论的电路元件参数都是指突出元件主要电磁性能的理想参数，如电感线圈只考虑其储存磁场能量的性质，认为是纯电感元件，其电路参数为电感量。同理，电阻元件只考虑消耗电能的性质，其参数为电阻；电容元件只考虑储存电场能量的性质，其参数为电容。

电阻元件

如下图所示是常用电阻元件及符号，电阻元件是消耗电能的元件，所以它是耗能元件。

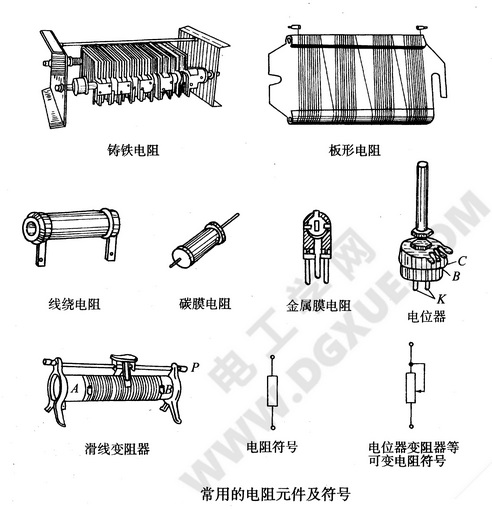
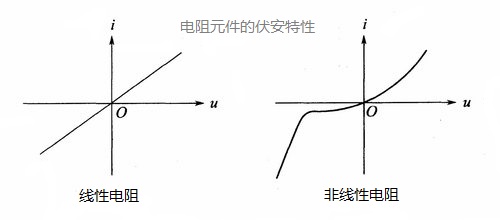
电阻元件分为线性电阻元件和非线性电阻元件。线性电阻的伏安特性如下左图所示，它是一条通过坐标原点的直线，直线的斜率就是电阻值R，这是一个常数。非线性电阻的伏安特性右图所示，是一条曲线，其电阻值R随电压或电流的变化呈非线性变化。半导体二极管是非线性电阻。

电阻元件的电流和电压总是同时存在的，遵循欧姆定律，u=iR，即任何时刻电阻的电压都是由该时刻流过电阻的电流决定的。当流过电阻的电流突然改变时，其电压也会突然改变；反之，当加在电阻上的电压突然变化时，通过电阻的电流也随之突变。因此将电阻上的电压或电流突然变化的现象称为跃变或突变。

某一瞬时，若电阻上的电压为u，流过的电流为i，此时电阻消耗的功率为：

 

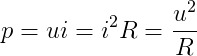
这个功率称为瞬时功率，它永远是正值，单位为瓦特（w）或千瓦（kW）。

在电路中，电阻将从电源吸收的电能全部转换成热能，电阻是耗能元件，电阻的耗能过程是不可逆的。在0~t的一段时间内，电阻消耗的电能可用下式表示：

若电阻R上流过的是直流电流I，其电压为U，电阻消耗的电能为：

 

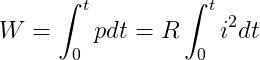
电能的单位是焦耳（J），工程上通常以瓦•秒（W•s）或千 瓦•小时（kW•h），俗称为度，作为计算电能的单位。

人们正是利用了电阻吸收电能转换为热能的这种特性，制造了电烙铁、电炉等用电设备。

电容元件

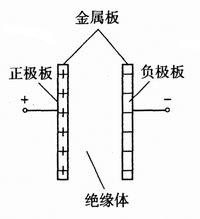电容元件电容器是由绝缘材料隔开的两个金属导体组成的，最常见的电容器是平行板电容器，由两块相互绝缘的平行金属板构成，如右图所示。在电容器两端外加直流电压金属板上积累的电荷量为Q，则电容器的电容量（或称电容）C为：

或写成：Q=CU_C

电容C是一个常数，它与金属板的面积大小、两板间的距离和绝缘材料有关，而与金属板的材料无关。从上式可以看出，电容两端的电压越高，它积累的电荷越多，电容器正、负极板上总是积累等量的相异电荷。

电容的单位为法拉（F），简称法。

工程上更多使用的单位是微法（1μF=10^-6F)和皮法（1pF= 10^-12F)。

 

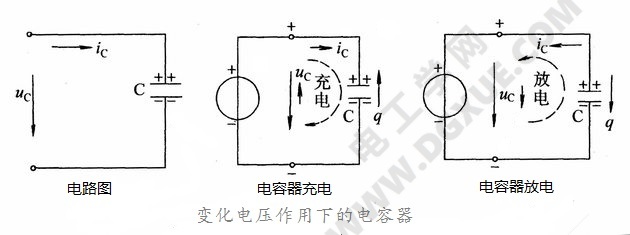
若加在电容器两端的电压U_c变化时，则电容器积累的电荷亦跟着变化，如上左图所示。电荷流动就意味着产生电流，电容端电压增高时，电容积累的电荷量增加，此时电容器充电；反之，端电压下降，电容器积累的电荷量减少，电容器放电。电容器储存的电荷与所加电压有如下关系：

q=Cu_c 或 C=q/u_c

将上面的公式代入电流的定义式，得：

 

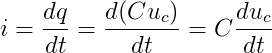
上述公式是在u_c和i参考方向一致时得出的，若u_c和i参考方向相反，式上公式前面要加负号。上式表明，电容电流与电容外加电压变化率成正比关系。

当电容器两端外加电压变化时，电路中就有电流流过，实际上电流并不能通过电容器金属极板之间的绝缘体。在上面的电容器充电图中，电容器的外加电压由电压可变的电源供给。当外加电压增大时，就有电流i (正电荷移动）从外加电压正端流入电容器的正极板，使正极板的电荷量q增加。正极板上的正电荷增多了，因静电感应在负极板上会产生等量负电荷而达到相应的平衡，而这时负极板上多余的负电荷就被排斥，从负极板流出，经外电路回到外加电源的负极，从而形成了充电电流的闭合回路，如中间的图（电容器充电）所示。反之，u_c减小时，则q减少，电容器正极板上多出的正电荷只好流出电容器，回到电源的正极，如上右图（电容器放电）所示。为了保持两极板上电荷的平衡，于是有一相等的正电荷从外加电源的负极流入电容器的负极板来中和掉多余的负电荷，从而形成了放电电流的闭合回路。这就是变化电流通过电容 器的物理本质，故电容电流是位移电流。

应注意，当电容两端电压u_c不变化时，即du_c/dt=0，电容电流亦为零，即电容在直流电路中相当于开路。

电容器的瞬时功率与电能：

瞬时功率：

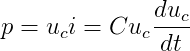
瞬时电能：

 

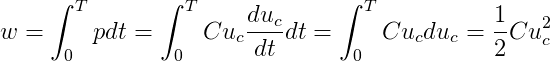
瞬时功率公式和瞬时电能公式说明，当外加电压u_c变化时，两极板间的能量也是变化的。当u_c增加时，p为正值，电容吸收电功率，其储存的电能增加，这增加的能量是电源提供的，此时电容器相当于负载；反之，当以减小时，p为负值，电容器极板上的电荷减小，其储存的电能也减少，这减少的能量又到哪里去了呢？

从电容器防电图可以看出，此时电源的极性或外加电压u_c的参考方向并没有改变，而电容器放电电流的方向与充电电流的方向正好相反，是从电源的正极流入，负极流出，这时电源成了一个接受电能的负载，电容器储存的电能以放电的方式返回给电源了。这说明在电压变化过程中，电容器并没有消耗掉电能，只是与电源之间进行能量的交换，这种交换是可逆的。由于电容器能将电能储存起来，而不会消耗掉，故电容称为储能元件。

电感元件

用金属导线绕成的线圈就是电感元件，简称电感，其外观形状如下图所示，其中“铁芯线圈”图是电工与电子技术中常用的小型电感元件及其电路图形符号。

 

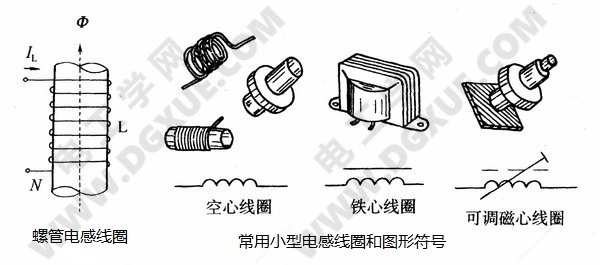
在N匝电感线圈两端通入直流电流IL，在线圈里即会产生磁通Φ，则线圈的自感系数L为：

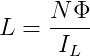
或者写成：NΦ=LIL

式中的NΦ称为磁链。电感的大小与线圈的几何尺寸、绕法和线圈内的磁性材料有关。如线圈内部有铁心，则电感L不是常数，称非线性电感。从上式中可知，当电感L为常数时，磁通Φ与电流I成正比例关系，这样的电感称为线性电感。磁通方向与电流的方向应符合右手螺旋定则。

电感的单位为亨利（H），简称亨，也可用毫亨（mH）， 1mH=10^-3H，或微亨（μH)，1μH=10^-6H。

若通入N匝电感线圈的电流iL是变化的，则线圈中的磁通Φ也是变化的，线圈的磁通变化率与电流变化率之间有下列关系式：

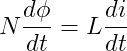
上式表面，通过电感线圈的电流若有增减变化，磁通量亦有增减变化。根据电磁感应定律，在线圈上会产生感应电动势e_L，它与磁通量对时间t的变化率的负值成正比，即：

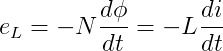
此感应电动势是因为通入线圈的电流变化而产生的，故称为自感电动势。

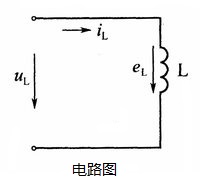根据右手螺旋定则，自感电动势的参考方向应与电流的参考方向一致，如右图所示，则上式中的负号表明，自感电动势总是反对电流变化的。其物理解释是，在下图中，电流i L增大，磁通φ增加，此时电流变化率di与dt之比大于零，为正值，说明线圈磁场储存的能量增加，线圈是负载，从电源吸收电能。由上e_L公式可知，e_L为负值，e_L的实际方向是反对电流增大的，如下图所示。反之，电流iL减小，磁通φ减小，电流变化率：di与dt之比小于零，为负值，说明线圈磁场储存的能量减少，这时线圈向电源提供电能。上式中的e_L为正值，e_L的实际方向是反对电流减小的，如下图所示。

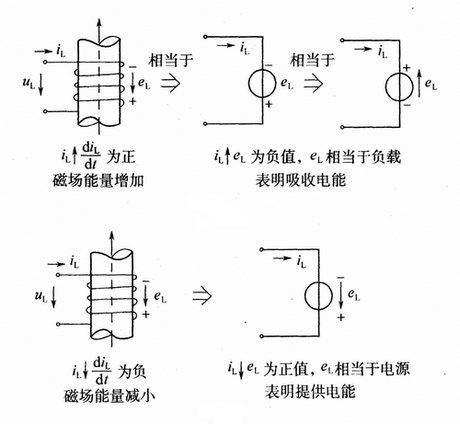
弄清楚了自感电动势e_L的产生和作用后，就可找出外加电压u与自感电动势e_L的关系。在第一个电路图中，由于电压的方向为电位降低的方向，而电动势的方向为电位升高的方向，即u和e_L的方向相反，所以有：

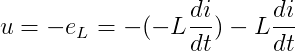
（公式后面，大写L前面的负号是等于号）

上式表面，电感线圈两端的电压等于自感电动势的负值，换言之，当u、e_L、i参考方向一致时，并且与磁通Φ的关系符合右手螺旋定则时，线圈的端电压u与流过的电流i可由上式表示。显然，当通过线圈的电流恒定不变即为直流电流时，自感电动势为零，相应底线圈两端的电压uL也为零。所以说电感线圈在直流电路中，相当于短路。

电感线圈的瞬时功率与电能的关系：

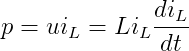
瞬时电能关系：

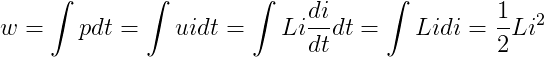
上两式表面，通过电感线圈的电流变化时，电感线圈的能量也是变化的，当iL增加时，磁场增强，磁场储能的能量增加，这部分能量必然由外电源提供；反之，当电流iL减少时，磁场削弱，磁场储能的能量减少，多余的磁场能量按电磁感应定律产生一个与电流参考方向相同的自感电动势。所以说，电感中磁场储能与电源电能之间的交换时可逆的，所以电感为储能元件。

通过点无源元件的分析可知，电阻是耗能元件，不与电源交换能量。电容、电感时储能元件，可以与电源交换能量。电容以电场形式储能。而电感则以磁场形式储能。