负载星形连接的三相电路及计算

电力系统中，用电设备种类繁多，既有三相用电设备，如三相电动机、大功率三相电炉等；也有单相用电设备，如交流电焊机、日光灯、家用电器等。用三相电源供电时，首先电源的电压应与设备的额定电压相同；其次应力求使三相负载对称，将各单相负载尽可能均匀地分接到三相电源上，使各相负载阻抗大小相等，阻抗角相同，即各相负载的性质相同，故称这种负载为三相对称负载，如图下图所示。

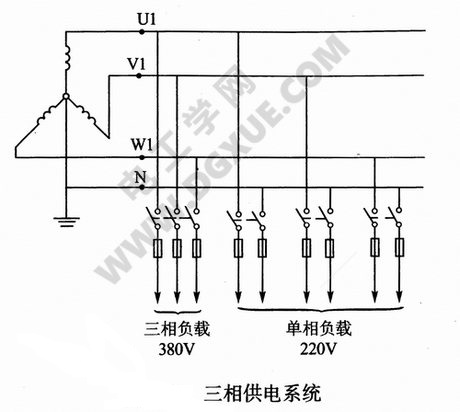
若三相负载不对称，即阻抗大小不同或阻抗角不等的三相电路称不对称三相电路。三相电路的计算一般是在已知三相电源电压和负载参数情况下求三相负载的电压、电流和功率的。

负载星形连接电路

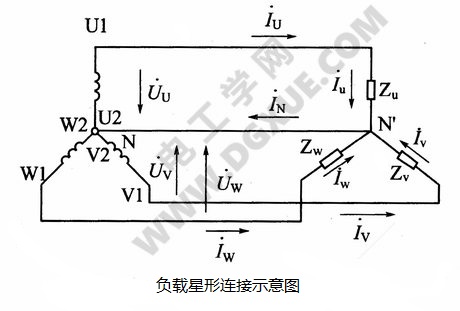
上图所示为负载星形联结的三相四线制电路图。三相负载Z_u、Z_v、Z_w的一端连成一点N’，即接到电源中性线N线上，每相负载的另一端分别与电源的三条相线U1、VI、W1相接。此时每相负载上流过的电流称相电流，用符号$\dot{I}_{u}$、$\dot{I}_{i}$、$\dot{I}_{w}$表示；火线上流过的电流称为线电流，用符号$\dot{I}_{U}$、$\dot{I}_{V}$、$\dot{I}_{W}$表示；中线上流过的电流称中线电流，用符号$\dot{I}_{N}$表示。此时相电流：

$$\dot{I}_{u}=\frac{\dot{U}_{U}}{Z_{u}} ~,~ \dot{I}_{v}=\frac{\dot{U}_{V}}{Z_{v}} ~,~ \dot{I}_{w}=\frac{\dot{U}_{W}}{Z_{w}}$$

星形连接时线电流与相电流为同一电流，即：

$$\dot{I}_{U}=\dot{I}_{u} ~,~ \dot{I}_{V}=\dot{I}_{v} ~,~ \dot{I}_{W}=\dot{I}_{w}$$

中线电流：

$$\dot{I}_{N}=\dot{I}_{u}+\dot{I}_{v}+\dot{I}_{w}=\dot{I}_{U}+\dot{I}_{V}+\dot{I}_{W}$$

当三相负载对称时

即Z_u=Z_v=Z_w=|Z|∠φ，只要计算出一相电流，其他两相电流便可知。若只计算$\dot{I}_{u}$，其大小：

$$I_{u}=\frac{U_{U}}{|Z_{u}|}$$

初相位角：

$$\varphi _{u}=arctan\frac{X_{u}}{R_{u}}$$

则$\dot{I}_{v}$、$\dot{I}_{w}$的大小与$\dot{I}_{u}$相同，初相位角分别为$\varphi _{v}=\varphi _{u}-120^{\circ}$，$\varphi _{w}=\varphi _{u}+120^{\circ}$。

此时，中线电流$\dot{I}_{N}=0$，既然中线没有电流流过，可以将中线去掉，电路便成为对称负载星形连接的三相三线制电路。如下图a所示。对称负载星形连接时电压、电流相量图如b所示。

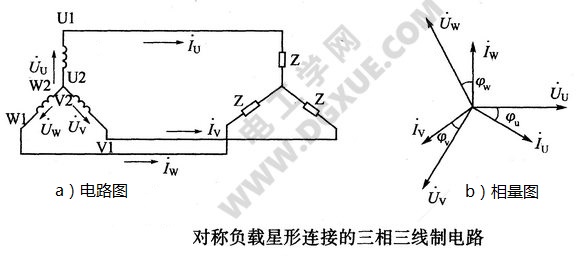
当三相负载不对称时

即Z_u≠Z_v≠Z_w，此时应该一相一相分别计算，各相电流的有效值为：

$$I_{u}=\frac{U_{U}}{|Z_{u}|} ~,~ I_{v}=\frac{U_{V}}{|Z_{v}|} ~,~ I_{w}=\frac{U_{W}}{|Z_{w}|}$$

各相负载电流与电压之间的相位差为：

$$\varphi _{u}=arctan\frac{X_{u}}{R_{u}} ~,~ \varphi _{v}=arctan\frac{X_{v}}{R_{v}} ~,~ \varphi _{w}=arctan\frac{X_{w}}{R_{w}}$$

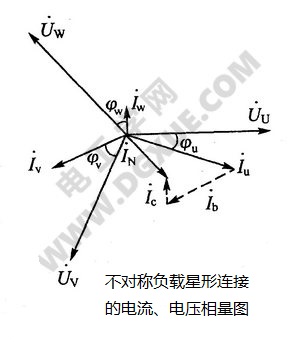中线电流：

$$\dot{I_{N}}=\dot{I_{u}}+\dot{I_{v}}+\dot{I_{w}}\neq 0 $$

中线有电流流过，计算时中线绝对不能去掉，电路便成为三相四线制电路。不对称负载星形连接时电压、电流相量图如下图所示。

算一算

题：三相对称负载星形连接，每相负载的R=10Ω，X_L=15Ω，接到三相电源上，已知$u_{UV}=380\sqrt{2}sin(\omega t+30^{\circ})V$，试求个相线电流。

解：因为负载对称，所以“只算一相，推知其他”的方法计算，现在只计算U相。U相电压的大小：

$$U_{P}=\frac{U_{UV}}{\sqrt{3}}=\frac{380}{\sqrt{3}}=220V$$

相电压$U_{u}$在相位上滞后线电压$u_{UV}$为30°，所以：

$$u_{u}=220\sqrt{2}sin\omega tV$$

U相得阻抗

$$Z_{u}=R+jX=10+j15\Omega $$

其中

$$|Z_{u}|=\sqrt{R^2+X^2}=\sqrt{10^2+15^2}=18\Omega $$
$$\varphi _{u}=arctan\frac{X}{R}=arctan\frac{15}{10}=56.3^{\circ}$$

U相的电流

$$I_{u}=\frac{U_{P}}{|Z|}=\frac{220}{18}=12.2A$$
$$i_{u}=12.2\sqrt{2}sin(\omega t-56.3^{\circ})A$$

同理推算出

$$ \begin{align}i_{u} & =12.2\sqrt{2}sin(\omega t-56.3^{\circ}-120^{\circ})\\ & =12.2\sqrt{2}sin(\omega t-176.3^{\circ})A\end{align}$$
$$ \begin{align}i_{w} & =12.2\sqrt{2}sin(\omega t-56.3^{\circ}+120^{\circ})\\ & =12.2\sqrt{2}sin(\omega t+63.7^{\circ})A\end{align}$$

中线电流：

$$i_{N}=i_{u}+i_{v}+i_{w}=0$$