电路的暂态过程：产生原因、利用等概念

前面三章的课程中我们讨论的是电路在给定条件下的稳定工作状态，即电路中的电压、电流值是稳定不变的（交流电路是指交流电压、电流的最大值)。但当电路从一个稳定状态到另一个稳定状态时会经历一个变化过程，过程时间可能很短（一般以毫秒或微秒计），此变化过程称暂态过程，又称过渡过程或瞬变过程。研究电路的暂态过程在电工、电子技术上是很有用的。

从本节开始只分析RC电路（电阻、电容串联电路)、RL电路（电阻、电感串联电路）与直流电源接通和分断时的暂态过程，重点是：

电路暂态过程中电压、电流随时间变化的规律；

影响暂态过程快慢的因素：时间常数。

暂态过程的产生于原因

工程上人们会有这样的概念：电动机从停止状态（一种稳定状态）启动时，其转速是从零逐渐增加，经过一段时间后，最后达到某个转速而稳定运行（另一种稳定转速）；当电动机停车时，其转速也是从某稳定转速逐渐减小，经过一段时间后，最后到零。在含有电容和电感的电路中，亦有类似的现象。

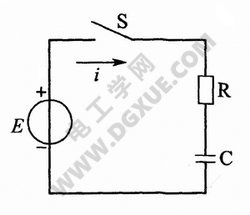
如右图所示电路，开关s未闭合图前，电容器未充电，$u_{C}=0,i=0$，电路处于一种稳定状态。将开关S闭合，电容器C开始充电，其两端压由零逐渐升高，电路中有电流i经过，一段时间后，当电容两端电压等于电源电动势，即$u_{C}=E$时，电容器端电压不再升高，与此同时，电路电流i也由最大值下降为零，电容器充电完毕，此时电容器处于另一个稳定状态。电容器的端电压从零增大到E，电流从最大值下降到零的变化过程，都需要一段时间，即电容端电压变化过程是一个渐变过程。如果电路中只有电阻元件，则从一个稳态到另一个稳态是以跃变形式出现的，即不需要时间。

电动机从某一转速下降为零之所以只能渐变，是因为电动机在转动过程中储存的动能不能瞬间耗尽，即表征动能的转速不能跃变。当有电容、电感元件的电路进行换路，也就是接通、切断、短路、电压改变或参数改变时，会使电路中的能量发生变化，而能量的变化是不能跃变的，在电感元件中储存的磁能$\frac{1}{2}Li_{C}^{2}$在换路时不能跃变，所以电感电路中的电流$i_{L}$不能跃变；

在电容元件中储存的电能$\frac{1}{2}Cu_{C}^{2}$在换路时不能跃变，所以电容元件的端电压$u_{C}$不能跃变。综上所述，电路的暂态过程是由于储能元件的能量不能跃变而产生的。

研究暂态过程的意义

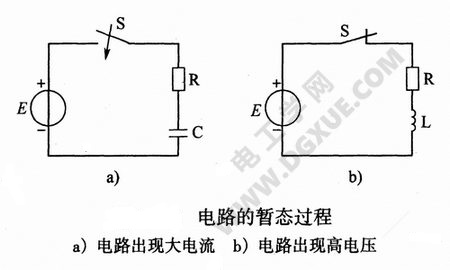
但下图a所示电路中，当开关S合上时，电路中可能出现较大电流，损坏设备（其原理在下面叙述）；

图b电路中，当开关S打开时，在开关S的触点间会产生较高电压，可能击穿空气，产生电弧，引起触点烧坏等。所以，应利用电路工作的暂态过程为电气工程服务，对其有害的一面应加以防止克服，这些就是研究电路暂态过程的原因。

换路定则和暂态过程初始值的确定

在含有电容元件、电感元件的电路进行换路时，根据其能量不能突变的原理，就得到换路定则，并利用换路定则来确定暂态过程在开始瞬间电路电流和各元件上电压的初始值。

若以换路瞬间作为计时起点，令此时t=0,换路前终了瞬间以$t=0_{-}$表示，换路后初始瞬间以$t=0_{+}$表示，$0_{-}$和$0_{+}$在数值上都等于零。换路定则的内容是：从$t=0_{-}$到$t=0_{-}$瞬间，电容元件上的电压和电感元件中的电流都不能跃变。用数学式表示为：

$$u_{C}(0_{-})=u_{C}(0_{+})$$
$$i_{L}(0_{-})=i_{L}(0_{+})$$

换路定则是用来确定换路瞬间电路中电流和各元件上电压初始值的依据。先由$t=0_{+}$时，得到$u_{C}(0_{-}),i_{L}(0_{-})$而后由$t=0_{+}$的电路在已求出的$u_{C}(0_{+}),i_{L}(0_{-})$的条件下求解其他电流和电压的初始值。

练一练

问题：右图所示的电路，电容C=10F未充电，R1=5kΩ，R2=2kΩ，电压源E=10V，求开关S合上瞬间各支路的电流。

解题：开关S合上瞬间，对R1支路有：

$$i_{1}(0_{+})=\frac{E}{R_{1}}=\frac{10}{5\times 10^3}=2mA$$

对R2C串联支路，根据换路定则有：

$$u_{C}(0_{-})=u_{C}(0_{+})=0$$

所以:

$$ \begin{align} i_{2}(0_{+}) & =\frac{E-u_{C}(0_{+})}{R_{2}}\\ & =\frac{E}{R_{2}}\\ & =\frac{10}{2\times  10^3}\\ & =5mA \end{align}$$

可以看出，此时的电容相当于短路。所以总电流为：

$$i(0_{+})=i_{1}(0_{+})+i_{2}(0_{+})=2+5=7mA$$