RC串联电路的暂态过程：充电、放电、时间常数

RC串联电路的充电过程

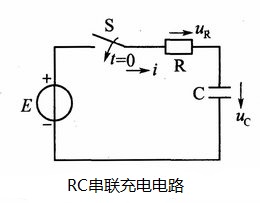如右图所示的电路中，开关S没有合上时，电容两端没有电压，即$u_{C}(0_{-})=0$，电路中的电流i=0。在合上S的瞬间到电容电压为E的暂态过程中，根据KCL，对回路可列出下列电压方程：

$$E=u_{R}+u_{C}=iR+u_{C}$$

根据前文《电路中的无源元件：电阻、电容和电感元件》电容部分所列公式带入上式可得出：

$$RC\frac{du_{C}}{dt}+u_{C}=E$$

此方程为一阶常系数线性微分方程，解方程得到电容电压的变化规律为（省略计算过程）：

$$u_{C}\tag{1}\label{1}=E-E_{e}^{-\frac{t}{RC}}=E(1-e^{-\frac{t}{RC}})$$

电路电流的变化规律为：

$$i=\frac{E}{R}e^{-\frac{t}{RC}}$$

电阻上电压的变化规律为：

$$u_{R}=iR=\frac{E}{R}e^{-\frac{t}{RC}}\times R=Ee^{-\frac{t}{RC}}$$

从公式中可以得出：RC串联电路在充电过程中，电容端电压随时间按指数规律逐渐增大，经过一段时间后，电容电压与电源电动势相等，电容充电完毕；而电路电流、电阻电压则随时间按指数规律逐渐减小到零。

$u_{C},i,u_{R}$的变化曲线如下图所示。

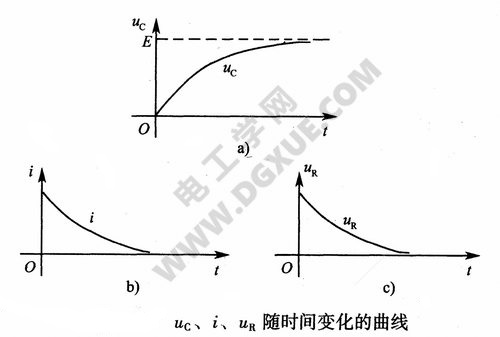
需要指出，在换路水煎，电容电压$u_{C}$不会发生跃变，$u_{c}(0_{+})=u_{C}(0_{-})$，电压是连续变化的。但是电容电流却在此瞬间发生了跃变。$i_{C}(0_{-})=0,i_{C}(0_{+})=\frac{E}{R}$这是因为电容电流与电容电场能量$W_{C}$无关。电容电流改变不会使电容电场能量发生跃变，故电容电流在换路瞬间是可以跃变的，这并不违反换路定则。

RC串联电路的放电过程

如右图所示的电路中，开关S先在位置1，使电容器充电到$u_{C}=E$。在$t=0$时，将开关S由位置1拨到位置2，使RC电路与电源断开，此时电容器C对电阻R放电。当开关S拨到位置2后的一瞬间，根据换路定则，电容电压仍保持为换路前一瞬间的值，即$u_{C}(0_{+})=u_{C}(0_{-}=E)$，接着电容就开始放电，电容电压从E值开始连续减小。在电容放电过程中，.储存在电容器极板上的电荷连续减小，电路中的放电电流i也随着电压的减小而减小，最后，电容中储存的电荷放尽，电容电压为零，电路电流i亦为零，这时电路达到了新的稳态，$u_{C}=0,i=0$

当开关合到位置2的瞬间到电容端电压为零的暂态过程中，根据KVL，对电路可列出如下电压方程：$u_{C}+i_{R}=0$

因i的参考方向与$u_{C}$参考方向相同，故有：

$$i=C\frac{du_{C}}{dt}$$

将上式代人电压方程，整理后可得：

$$RC\frac{du_{C}}{dt}+u_{C}=0$$

此方程为一阶常系数线性齐次微分方程，解方程得电容电压的变化规律为（求解过程省略)：

$$u_{C}\tag{2}\label{2}=Ee^{-\frac{t}{RC}}$$

电路电流的变化规律为：

$$i=-\frac{E}{R}e^{-\frac{t}{RC}}$$

电阻R的电压变化规律为：

$$u_{R}=-Ee^{-\frac{t}{RC}}$$

从上几式表明，RC串联电路放电过程中，其端电压随时间按指数规律连续衰减到零，电路电流、电阻电压亦按指数规律逐渐减小到零。放电曲线如右图所示。

时间常数

在上两式$\eqref{1} ,\eqref{2} $中，RC乘积的量纲[欧（Ω）×法（F）=欧（Ω）×库（C）/伏（V）=欧（Ω）×（安（A）×秒（s）/伏（V））=秒（s）]为s，是时间的单位，所以称其为时间常数，并用τ表示。时间常数的大小决定了充电、放电过程的快慢。在E相同，R、C数值不同的两个充电电路中，尽管电容电压、电路电流由相同的初始值变化到相同的终值，但暂态过程的时间是不同的，如下右图所示。时间常数大，即R大或C小的电路中，充电速度快，充电时间就短。这是因为电容器上的电压与极板上的电荷量成正比，即$u_{C}=Q/C$，如要求充电到相同电压数值E时，电容C较大时充入的电荷Q就多，因此时间要长一些；另一方面，如果充电电路的电阻R大，充电电流i必然会小一些，电容到达同样的端电压积累同样的电荷所需的时间也会长一些。同理，在放电电路中，电容C大，储存的电荷多，放电时间必然较长；电阻R大，放电电流就小，储存的电荷多，放电时间必然较长；电阻R大，放电电流就小，放出同样数量的电荷时间也就要长一些。

时间常数也可做如下说明：RC串联电路充电过程中，经过时间$t=τ=RCs$后，电容电压恰好上升为$(1-e^{-1})E=63.2%E$，如上左图所示。因此时间常数τ可以看成是电容器充电过程中端电压增大到63.2%E时所需的时间。放电过程中，τ是电容电压已下降了63.2%E时所需要的时间。

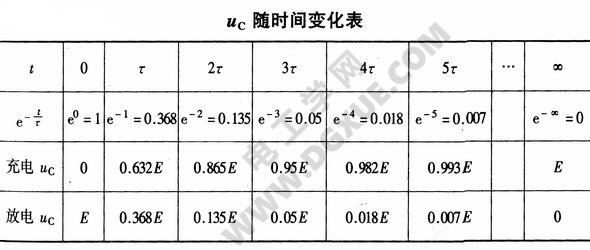
从上两式$\eqref{1} ,\eqref{2} $可知，理论上，按指数规律电容器的充电、放电过程，必须经过无限长的时间，暂态过程才结束，而进入一个新的稳定状态。但是当暂态过程经历时间为（3~5）倍τ后，电容端电压已达到95%~99.3%的电源电动势E，因此将（3~5）倍τ作为暂态过程经历的时间。下表列出了电容器充电、放电时$u_{C}$随时间变化的情况。