复杂直流电路的计算方法总结
本课主要研究复杂电路的分析计算方法。为了便于读者理解、掌握这些方法,在此以直流复杂电路为例进行讨论这些方法对交流电路同样适用,只是表达形式不同而已。
支路电流法
支路电流法是以支路电流为未知数,直接应用基尔霍夫两个定律列方程求解支路电流的方法。一下图为例,说明支路电流法的解题步骤。
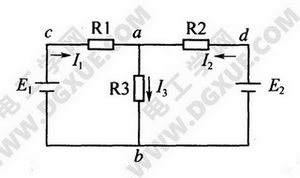
选定各支路电流的参考方向,并标在电路上参考方向是可以任意选定的。一个复杂电路若有m条支路,就有m个未知电流,需要列出m个方程式联立求解。右图所示电路有三条支路,三个电流;I1、I2、I3就是未知电流,设定参考方向后标在图上,列出三个独立方程式求解,即可得出各电流值。
根据KCL列出各节点独立的电流方程当电路中有n个节点时,只能有(n-1)个电流方程是独立的。因为最后一个节点的电流方程可以由前(n-1)个电流方程推出,故不是独立方程。上图电路有a、b两个节点,只能列出一个独立电流方程(2-1=1)。取a点来列电流方程,按图中标出的电流参考方向列出:
I1+I2=I3
根据KVL列出独立的电压方程对于有m条支路、n个节点的电路,独立的电压方程数为m-(n-1)个。所谓独立电压方程是在选择回路时应包含一条或一条以上新支路,这条新支路是在其他已列过方程中从未出现过的,否则列出的方程就不是独立方程。上图中有三条回路,两个节点,只能列出两个独立回路方程[3-(2-1)]。取回路cadbc、adba,按顺时针方向巡行,可列出方程。
E1-E2=I1R1-R2R2
E2=I2R2+I3R3
解联立方程式,即可求出各支路电路,如果求出的支路电流为负,说明该支路电路的实际方向与设定的参考方向相反。
校验结果是否正确:可用功率平衡或电压平衡关系进行校验。
叠加原理
叠加原理是线性电路的重要基本原理,它说明了线性电路中各个电源对电路的影响是独立的。正确掌握叠加原理能使我们进一步加深对线性电路的认识。
叠加原理的内容是:在线性电路中,所有独立电源同时作用时,在每一条支路中产生的电流或电压,等于各个电源单独作用时在这条支路中产生的电流或电压的代数和。
需要注意的是,当一个电源单独作用时,其他电源则应置零。对恒压源应用短路代替,表示该恒压源处是零电压;对恒流源用开路代替,表示该恒流源处是零电流。
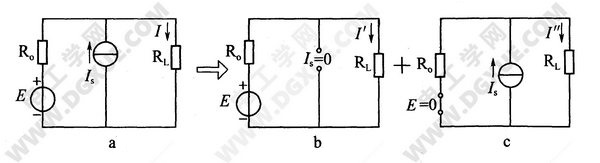
如上图所示电路中,电压源与恒流源共同作用在电阻RL上,流过电流I。这个电流I可以认为是由电压源单独作用时在上产生的电流分量I'(此时恒流源应开路,如图b所示)和恒流源单独作用时在RL上产生的电流分量I”(此时电压源应短路,内阻保留,如图c所示)的代数和,即I=I’+I”。
必须注意,支路电流叠加时应是各个电源单独作用时电流的代数和。当每个电源单独作用时产生的电流与原支路电流参考方向一致时取正号,相反时取负号。
叠加原理也可用于之路电压的叠加,但不能用于支路功率的叠加,因为功率是电流的二次方函数。
电压源和电流源的等效变换
真实电源不论是以电压源形式还是以电流源形式出现,对外电路(负载电路)都要输出电流和电压。所以对外电路来说,只要其端电压或流过的电流保持不变时,电压源或电流源对它们的作用是等效的。
真实电源的两种表示方法,如下图的虚线框中所示,a为电压源,b为电流源。当Is=E/R。或E=IsR0。时,两者对外电路是等效的。证明如下,把负载RL接入电路:
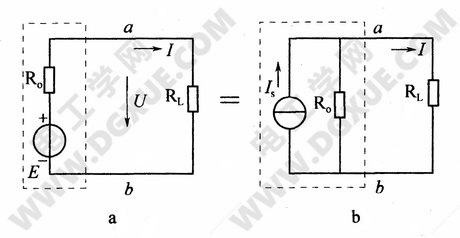 图a中:
图a中:
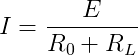
图b中:
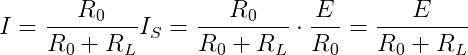
电流等效,则电压及功率也等效。所示式:
就是电压源与电流源等效互换的条件。也就是说,只要满足上式的条件,电压源与电流源就可以等效互换。
必须强调指出:
- 真实电源的等效互换,只是对外电路等效,对电源内部是不等效的。如上图所示电路中,若a点断开,则I=0, 电压源内阻Ro上无电流流过也不消耗功率,但电流源内阻R0上有电流Is流过,内阻是消耗功率的,可见电源内部是不等效的。
- 要注意电源的极性。因为它们对外电路产生电流的方向相同,所以电流源电激流流出的一端应与电压源的正极相对应。
- 恒压源与恒流源不能等效互换,因为恒压源在电流为任意值时,端电压始终与电动势相等,是恒定值,恒流源不具有这种性质;而恒流源的端电压为任意值时,输出电流始终等于电激流,是恒定值,恒压源也不具有这种性质。
- 与恒压源相并联的元件或支路,去掉与否,不影响外电路的计算。
- 与恒流源相串联的元件,去掉与否,不影响外电路的计算。
- 任何一个恒压源和某一个电阻(不一定是电源内阻)串联的电路,都可以等效为恒流源和这个电阻并联的电路;反之,任何一个恒流源和某一个电阻并联,也可以等效为恒压源和这个电阻串联的电路。这样变换对外电路的作用是一样的。
电压源与电流源的等效变换非常简便,用等效变换可以使复 杂电路的计算简化。
等效电源定理
等效电源定理包括戴维南定理和诺顿定理。在分析研究某些电路时,若只需要知道复杂电路中某一条支路的电流,能否找到一个简便的办法,避开解联立方程组或化简电路呢?等效电源定理可以帮助我们解决这类问题。
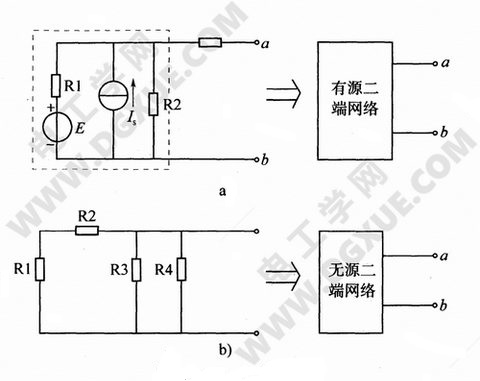
如果电路(或网络)只有两个引出端与外电路相联,这个电路叫做二端网络。二端网络内如含有电源的称有源二端网络;如不含电源的称无源二端网络,分别用下图a、b表示。
戴维南定理
戴维南定理指出:任何一个线性有源二端网络,对于外电路来说,都可以用一个电动势E和电阻Ro串联的电压源来代替,如图a、b所示。等效电压源的电动势E等于有源二端网络输出端开路时的开路电压U0,如下图c所示。图c中的U0与图a中的Uab是不相同的;等效电压源的内阻R0等于将有源二端网络内所有电源置零后(各恒压源短路、各恒流源开路)所得到的无源二端网络的输出端等效电阻,如图d所示。
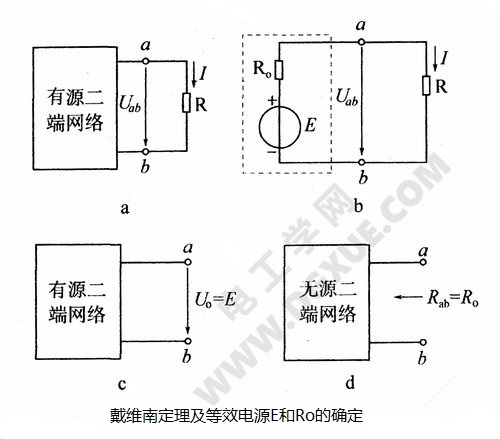
应用戴维南定理可将一个复杂的有源二端网络简化为一个简单的等效电压源。
诺顿定理
诺顿定理指出:任何一个线性有源二端网络对于外电路来说,都可以用一个电激流Is和内阻R0并联的电流源来代替,如下图a、b所示。等效电流源的电激流Is等于有源二端网络输出端短路时短路线上的电流,如图c所示,内阻R0等于有源二端网络内所有电源置零后(恒压源短路、恒流源开路)所得的无源二端网络输出端的等效电阻(即与戴维南定理的等效电阻一样),如图d所示。
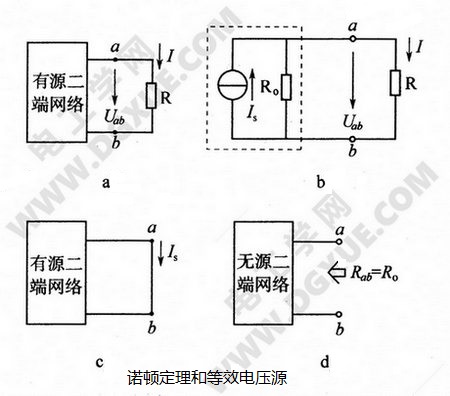
应用诺顿定理可以将一个复杂的有源二端网络简化为一个等效电流源。利用诺顿定理求解复杂电路的关键是正确求出有源二端网络的短路电流和无源二端网络的等效电阻。
看了本文的人还看了
- 视频:交流调压电路
- 视频:周期性非正弦电流电路的分析和计算
- 视频:RL电路的响应
- 视频:RC电路的响应
- 视频:阻抗的串联与并联
- 视频:R、L、C串联的正弦交流电路(1)
- 视频:正弦交流电压与电流
- 视频:非线性电阻电路分析
- 视频:电路的基本定理(4)
- 视频:电路的基本定理(3)
- 视频:电路的基本定理(2)
- 视频:电路的基本定理(1)
- 视频:电路的基本物理量及其参考方向(第二讲)
- 视频:电路的基本物理量及其参考方向(第一讲)
- 视频:电路的基本概念
- CLCπ型滤波、CRCπ型滤波电路
- RC串联电路的暂态过程:充电、放电、时间常数
- 电路的暂态过程:产生原因、利用等概念
- 功率三角形、阻抗三角形、电压三角形的比较
- 瞬时功率、有功功率、无功功率、视在功率讲解
- 单一参数正弦交流R、L、C(电阻/电感/电容)稳态电路
- 正弦交流电的电动势、电压和电流
- 实例:用桥式电路寻找电话线碰线故障地点
- 电路中电位的计算方法讲解
- 电路的基本定律:基尔霍夫电流定律和电压定律
- 电路中的无源元件:电阻、电容和电感元件
- 电路中的有源元件(电压源、电流源)
- 电路中的常用物理量:电流及方向、电动势、电功率等
- 高电压对绝缘电阻的影响:泄露电流
- 电动机定子绕组串联电阻自动切换降压启动电路接线图(二)
 鄂网公安备 42112502000017号
鄂网公安备 42112502000017号