电阻和电感串联的交流电路中的电功率公式及关系
本节课是上节课《电阻和电感串联的正弦交流电路中电压与电流的关系》的延续部分。
功率关系
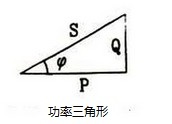 将电压三角形的每边乘以I就得到了如下右图所示的功率三角形,它表明了争先交流电路中有功功率P、无功功率Q和视在功率S之间的数量关系,也满足勾股定律。
将电压三角形的每边乘以I就得到了如下右图所示的功率三角形,它表明了争先交流电路中有功功率P、无功功率Q和视在功率S之间的数量关系,也满足勾股定律。
在R、L串联(即电阻和电感)交流电路中,只有R是耗能元件,故而电路的有功功率为:
![]()
由电压三角形可知,Uc=UcosΦ,所有,有功功率一般表示为:
![]()
上述公式中cosΦ称为电路的功率因素,它是表征交流电路工作状态的重要技术数据之一。
电感L只与电源交换能量,其无功功率为:
![]()
在上述两个公式中,乘积IU是电源供给电路的总功率,虽然UI具有功率的形式,但并不是电路中真正消耗的功率,它包含着有功功率和无功功率两部分。只有有功功率才是电路实际消耗的功率。所以乘积UI称为视在功率,用字母“S”表示,视在功率的单位为伏安(VA),或千伏安(KVA):定义式为:
![]()
由上右图所示功率三角形为一直角三角形,根据勾股定律:
![]()
由于纯电感只消耗无功功率,而电阻性负载消耗有功功率,所以在电感性负载交流电路中,衡量电能被利用来作有功功率的程度用功率因素cosΦ来表示。
从有功功率P=UIcosΦ的公式中,可以看出,在同样的视在功率UI情况下,Φ越小,cosΦ越大,P越大,电源所做的有功功率越多,电能利用程度就越高。
电灯是电阻性负载,功率因素最高,Φ为零,cosΦ=1.电动机的功率因素在满载时为0.7~0.8,轻载时更低,为了充分利用发电和变电设备的能力,提高功率因素是有重大意义的。
课后例题
例题:一只40W的日光灯,接入U=220V的正弦交流电源上,其cosΦ=0.5,球:电流I、视在功率S、无功功率Q。
思路:首先由课中提到的有功功率公式P=UIcosΦ,再带入上述一直数值可得出电流I=0.36(A),再由视在功率S=UI计算出功率S=79(VA)、同样的利用功率三角形得知的另一个勾股定律视在功率公式即可算出无功功率Q=68(Var)。
看了本文的人还看了
- 视频:周期性非正弦量的分解
- 视频:RL电路的响应
- 视频:三相功率
- 视频:正弦交流电路的频率与谐振(3)
- 视频:正弦交流电路的频率与谐振(2)
- 视频:正弦交流电路的频率与谐振(1)
- 视频:功率因数的提高
- 视频:复杂正弦交流电路的分析与计算
- 视频:R、L、C串联的正弦交流电路(2)
- 视频:R、L、C串联的正弦交流电路(1)
- 视频:单一参数元件的正弦交流电路
- 视频:正弦交流电的相量表示法
- 视频:正弦交流电压与电流
- CLCπ型滤波、CRCπ型滤波电路
- 电感、电容滤波电路
- 桥式整流滤波电路:电容滤波
- RL(电阻、电感)串联电路的暂态过程
- RC串联电路的暂态过程:充电、放电、时间常数
- 三相对称负载的有功功率和无功功率计算
- 功率因数的作用及提高
- 瞬时功率、有功功率、无功功率、视在功率讲解
- R、L、C串联和并联的正弦稳态电路
- 单一参数正弦交流R、L、C(电阻/电感/电容)稳态电路
- 正弦交流电正弦量的表示:相量表示法
- 正弦交流电正弦量三要素:频率、幅值、初相位
- 正弦交流电的电动势、电压和电流
- 正弦交流稳态电路
- 电路中的无源元件:电阻、电容和电感元件
- 电路中的常用物理量:电流及方向、电动势、电功率等
- 按电流原则控制转子串联电阻降压启动电路接线图解
 鄂网公安备 42112502000017号
鄂网公安备 42112502000017号